Seconda Legge del Moto nello Spazio - Moto Parabolico

---

Indichiamo la Ridefinizione della Parabola, come indicata nella Geometria Parametrica:

In un riferimento cartesiano (ortogonale) il luogo geometrico dei punti che distano dall'origine la somma algebrica di una costante p (p \(\in \mathbb{R^+} \)) ed una coordinata di tali punti,cioè (p\(\pm y \)) (y asse di simmetria) e (p\(\pm x \)) (x asse di simmetria), dà luogo ad una curva chiamata Parabola e l'Origine è detto Fuoco, se il campo di variabilità di tali coordinate è compreso tra \( ( -\frac{p}{2};+\infty ) \) e \( ( +\frac{p}{2};-\infty ) \). Dove p=parametro della parabola e p/2=distanza Vertice-Fuoco. Ad Esempio

\( (p+x)^2=x^2+y^2 \) dà la parabola per punti:\( \quad y^2=p^2+2 p x\quad\) e parametrica \(\begin {cases}(p+x)\cos\beta=x\\(p+x) \sin\beta =y \end{cases} \quad\) con l'origine nel fuoco.

La Parabola in forma Parametrica. Sia la Parabola Parametrica di Vag, con Origine posto nel Fuoco e in forma parametrica:

\(\frac{R}{\cos\alpha_1}=\frac{R}{\cos\alpha_1} \left(1-2\cos\alpha \right) \cos\beta+\frac{R}{\cos\alpha_1}\left(\pm 2\sqrt{\cos\alpha\left(1-\cos\alpha \right)} \right)\sin\beta; \;\;\) (**)
con \( \beta \) angolo al centro e con α angolo di riferimento di una circonferenza e con α₁=α e 2R=p=parametro della parabola. Il moto della parabola è dal vertice verso \(\infty\) se in coseno e da \(\infty\) al vertice se in seno.

La prerogativa di questa equazione è che se fermiamo α₁ ad un determinato valore (in Fig.F è α₁=33°), per cui R/cosα₁ diventa una costante, la parabola da quel punto in poi, ruoterà secondo una circonferenza con centro nell'Origine = Fuoco e raggio R/cosα₁. Tutto questo è indicato con il grafico di Fig.F Equazione del Moto degli Asteroidi  

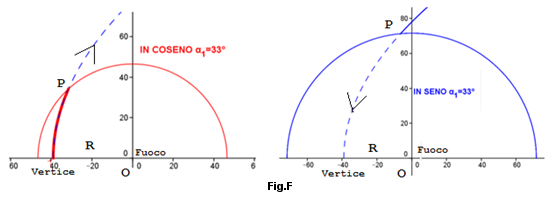
Vediamo il caso di \(OP= \frac{R}{\cos\alpha_1} \): P è il punto della parabola che per effetto di di forze esterne varia la sua velocità, passando da una traiettoria parabolica a quella circolare con la nuova velocità (Media) \(\;\; V^2=\frac{GM}{\overline{OP}}=\mathrm{cost.} \;\;\) e dove G è la costante di gravitazione ed M è la massa del Pianeta e OP il raggio. Tale moto Circolare giustifica la sua nuova posizione secondo la Prima Legge del Moto dei Pianeti.